Biography
I am a research engineer at Georgia Tech and the AI Institute for Advances in Optimization (AI4OPT), working with Pr. Pascal Van Hentenryck. My work focuses on optimization and machine learning and their application to power systems. I received my PhD in 2020 from Polytechnique Montréal, where I was advised by Prs. Andrea Lodi and Miguel F. Anjos.
- Mixed-Integer Optimization
- Power Systems
- Machine Learning
PhD in Applied Mathematics, 2020
Polytechnique Montréal
M.S., 2015
Ecole polytechnique
Experience
Responsibilities include:
- Project management
- Undergraduate and graduate students supervision
- Interactions with industrial partner
Recent & Upcoming Talks
Featured Publications
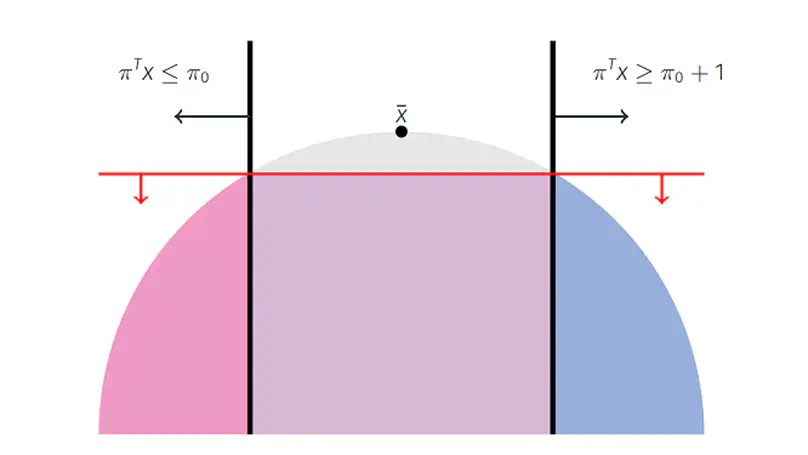
This paper studies disjunctive cutting planes in Mixed-Integer Conic Programming. Building on conic duality, we formulate a cut-generating conic program for separating disjunctive cuts, and investigate the impact of the normalization condition on its resolution. In particular, we show that a careful selection of normalization guarantees its solvability and conic strong duality. Then, we highlight the shortcomings of separating conic-infeasible points in an outer-approximation context, and propose conic extensions to the classical lifting and monoidal strengthening procedures. Finally, we assess the computational behavior of various normalization conditions in terms of gap closed, computing time and cut sparsity. In the process, we show that our approach is competitive with the internal lift-and-project cuts of a state-of-the-art solver.
